概诉
阿姆达尔定律
什么是阿姆达尔定律
阿姆达尔定律(英语:Amdahl’s law,Amdahl’s argument),一个计算机科学界的经验法则,因吉恩·阿姆达尔(Gene Amdahl)而得名。它代表了处理器平行运算之后效率提升的能力。
1967年计算机体系结构专家吉恩.阿姆达尔提出过一个定律阿姆达尔定律,说:在并行计算中用多处理器的应用加速受限于程序所需的串行时间百分比。
举两个例子说明这个问题:
-
譬如说,你的程序50%是串行的,其他一半可以并行,那么,最大的加速比就是2。不管你用多少处理器并行,这个加速比不可能提高。在这种情况下,改进串行算法可能比多核处理器并行更有效。
-
假设某一功能的处理时间为整体系统运行时间的60%,若使该功能的处理速度提高至原来的5倍,则根据阿姆达尔定律,整个系统的处理速度可提高至原来的多少倍?
阿姆达尔定律规则
加速比
优化前系统总耗时To(old),优化后系统总耗时Tn(new),为加速比
1 | S =To/Tn |
原系统中能够改进的部分占总部分的比例:C
原系统中能够改进的部分占总部分的比例,也可以说能够改进部分运行时间占总系统运行时间的比例,比如上文所说的,加入的你程序100%是并行的,如果将50% 改成并行(或者其他能提高速度的方式),那么 C = 50%
系统的提升比例St
比如 系统比原系统提升了5倍 这是个比例(St=5)
公式如下
1 | S = To/Tn = 1 / ((1-C) + C/St) |
计算
那么我们来回答第一个问题
你的程序50%是串行的,其他一半可以并行,那么,最大的加速比就是2。不管你用多少处理器并行,这个加速比不可能提高。
根据公式得到
1 |
|
也就是说你把另一半程序优化的比原来提升多少倍,那么加速比,也就是说 你能提升的性能最大可能是原来的 2倍。
假设某一功能的处理时间为整体系统运行时间的60%,若使该功能的处理速度提高至原来的5倍,则根据阿姆达尔定律,整个系统的处理速度可提高至原来的多少倍?
1 | S = 1/((1 - 0.6 )+ 0.6 / 5) |
阿姆达尔定律原理
为了更好地理解阿姆达尔定律,我会尝试演示这个定定律是如何诞生的。
首先,一个程序可以被分割为两部分,一部分为不可并行部分B,一部分为可并行部分1 – B。如下图:

在顶部被带有分割线的那条直线代表总时间 T(1)。
下面你可以看到在并行因子为2的情况下的执行时间:
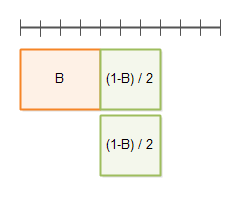
并行因子为3的情况:

我们假设不考虑其他因素,并行因子越大, 那么1 - B 所占用的时间越短,也就是图中略色的部分也就越短。
当我们 并行因子(也就是我们 将 1 - B 运行的速度提升 n 倍 n → ∞)提升无穷大。那么绿色的面积会越来越小,最后约等于0
那么我们程序的总时间将约等于 B 的时间。
因此我们得出结论:在并行计算中用多处理器的应用加速受限于程序所需的串行时间百分比。
总结
虽然阿姆达尔定律允许你并行化一个算法的理论加速比,但是不要过度依赖这样的计算。在实际场景中,当你优化或并行化一个算法时,可以有很多的因子可以被考虑进来。
内存的速度,CPU缓存,磁盘,网卡等可能都是一个限制因子。如果一个算法的最新版本是并行化的,但是导致了大量的CPU缓存浪费,你可能不会再使用x N个CPU来获得x N的期望加速。如果你的内存总线(memory bus),磁盘,网卡或者网络连接都处于高负载状态,也是一样的情况。
我们的建议是,使用阿姆达尔定律定律来指导我们优化程序,而不是用来测量优化带来的实际加速比。记住,有时候一个高度串行化的算法胜过一个并行化的算法,因为串行化版本不需要进行协调管理(上下文切换),而且一个单个的CPU在底层硬件工作(CPU管道、CPU缓存等)上的一致性可能更好。
参考
赞赏一下