算法 动态规划

算法探秘系列之动态规划（2）

背包问题

Posted by Jason Lee on 2019-05-30

背包问题

有N件物品和一个容量为V的背包。第i件物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使价值总和最大。

问题分类

  • 01背包问题 如果N个物品每个物品只能使用一次，则成为01背包问题
  • 完全背包问题 如果NN个物品每个物品可以使用无限次，则为完全背包问题

问题的解法

  • 暴力搜索解法（递归解法）
  • 动态规划解法
  • 优化后的动态规划（滚动数组，自下而上）

01背包问题

有N件物品和一个容量为V的背包。第i件物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使价值总和最大。 每件物品只能使用1次

问题分析

  • 设 C(i,w) 为 当物品有i个的时候, 且背包重量在 w 的情况下 取得的最大值。那么考虑第 i 个物品，无外乎两种可能：选，或者不选。
    • 不选的话，背包的容量不变，改变为问题 C(i -1, w)；
    • 选的话，背包的容量变小，改变为问题 C(i -1, w- w[i]) 。
      最优方案就是比较这两种方案，哪个会更好些：
      我们来看状态方程

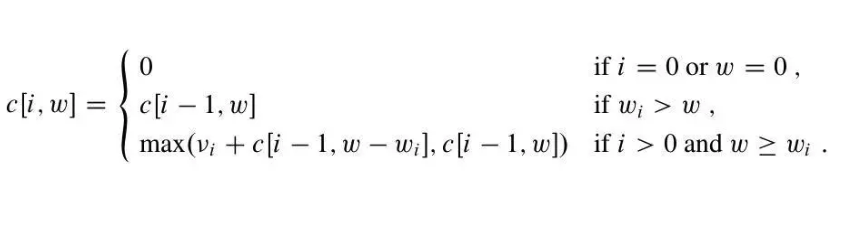
  • 如何理解这个方程：

    假设 我们有 c[3,4] 和 w [5,10] ,i[0,1] i 我们放每个元素的名称。

    首先对于0 这个元素 重量为5 价值为3。
    假设
    我们要求 C(1,5) 代表 在背包重量为5 的情况下 从 0,1中选择价值最大的。 直观的结果当让是3了。

  • 分析过程
    按照上述公式 当我要求 C(1,5) 的时候，对于1这个元素有两种求法

    • 1 这个元素被选中
    • 1 这个元素没有被选中

    如果1 被选中了，则背包的重量要减去1的重量10那么在接下来的问题就变成 在 C(0,5 - 10) + 4（4 是用于1已经被选中了，所以原问题就变成了在子问题基础上 加上 已经选中的价值） 但是 C(0, -5) 不可能存在，所以 1 不能选 所以 有了 C(0,5) 的子问题

  • 我们在看一个更复杂的例子：

    ps = [12,3,1,3,6]

    ws = [5,4,7,2,6]

    i = [0,1,2,3,4] （物品的代号）

    W = 10

    我们依旧定义问题 C(4, 10)
    根据公式，我们来公式

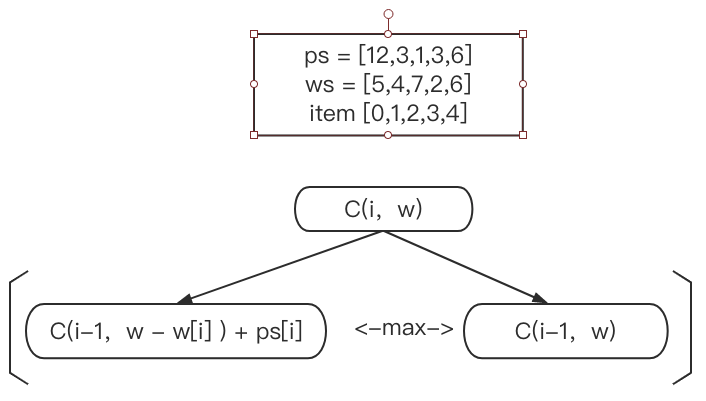
    下面是具体的分析过程
    4 被选中

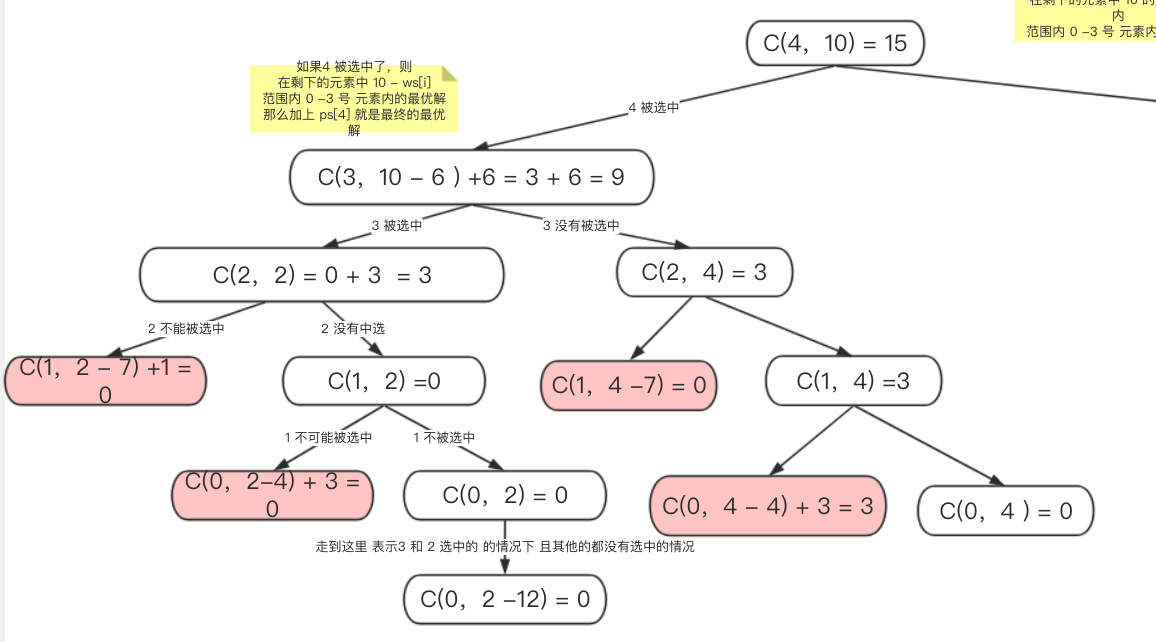
    4 没有被选中

    求C(4, 10)

    • 如果4 号元素被选中了，则进入子问题构成的问题
      C(4 -1, 10 - ws[4]) + ps[4]
    • 如果4 号元素 没有被选中，则进入第个子问题C(4 -1, 10
    • 这两个我们要取得最大的结果 才符合要求
    • 处理边界 当i 和v 有一个小于0 的时候 这个问题都是不存在的

代码实现

递归写法

1
2
3
4
5
6
7
8
9
10
# 0 -1 背包问题 
def package0_1(idx, v, w, ws, ps):
    if v >= w:
        return 0
    if idx > len(ps) - 1:
        return 0       
    # 如果选中该物品 太大 则放弃选中 原因就是 如果返回0 则会参与下边的运算max 会使得 ps[idx] + 0 会直接返回 ps[idx] 的值导致问题错误
    if ws[idx] + v > w:
        return package0_1(idx+1, v, w, ws, ps)
    return  max(ps[idx] + package0_1(idx+1, v + ws[idx], w, ws, ps), package0_1(idx+1, v, w, ws, ps))

运行结果

1
2
3
4
ps = [12,3,1,3,6]
ws = [5,4,7,2,6]
ret = package0_1(0, 0, 10, ws, ps) 
ret = 15

动态规划写法

  • 中间结果的保存

    由于我们的问题是C(i,w) i 和w 会有各种不同的取值 那么我们申请一个二维数组来保存中间计算的结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#   由于我们的问题是`C(i,w)` `i` 和`w` 会有各种不同的取值 那么我们申请一个二维数组来保存中间计算的结果
def package0_1_dynamic_1(idx, v, w, ws, ps):
    max_idx = len(ps)
    ret_mid = [[ None for i in range(w + 1)] for j in range(max_idx)]
    
    def package0_1_inner_1(idx, v, w, ws, ps):
        if v >= w:
            return 0
        if idx > max_idx - 1:
            return 0

        if ret_mid[idx][v] is not None:
            return ret_mid[idx][v]
        ret_tmp = 0
        if ws[idx] + v > w:
            ret_tmp = package0_1_inner_1(idx + 1,v, w, ws, ps)
        else:
            ret_tmp = max(ps[idx] + package0_1_inner_1(idx+1,v + ws[idx], w, ws, ps),package0_1_inner_1(idx+1,v, w, ws, ps))
        ret_mid[idx][v] = ret_tmp
        return ret_mid[idx][v]
    
    ret = package0_1_inner_1(idx, v, w, ws, ps)
    print(ret_mid)
    return ret

运行结果

1
2
3
4
ps = [12,3,1,3,6]
ws = [5,4,7,2,6]
ret = package0_1_dynamic_1(0, 0, 10, ws, ps) 
ret = 15
  • 优化分析
    如果我们打印 ret_mid
v/i 0 1 2 3 4 5 6 7 8 9 10
0 15 None None None None None None None None None None
1 9 None None None None 3 None None None None None
2 9 None None None 6 3 None None None 0 None
3 9 None None None 6 3 None 3 None 0 None
4 6 None 6 None 6 0 0 0 None 0 None

这个表格的意思是，当我们选中 背包选中0 的时候 且这个时候背包的总量为 0的时候 最大的价值 为15 既C（0，0）的含义
同理C(1,0)的意思是 没有选中 0 且 选中 1和 不选 1的价值最大的值

我们分析一下 如果我要求 C(i,w) 但是需要依赖于 C(i+1,?) 这里用? 表示只需要行数据。 那么需要上面数组 C(i+1,?) 的结果
也就是说 我们的 ret_mid[i] 要依赖于 ret_mid[i+1] 的结果 这个时候 我们的 ret_mid[i+1] 还没有被算出来
如果我们反转一下， 是否能计算将这个顺序 倒置一下，比如说让ret_mid[i] 依赖于 ret_mid[i - 1] 这样依赖，我们算到了ret_mid[0] 的时候，就可以被 ret_mid[1] 复用结果了。

我们来看一下代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#   由于我们的问题是`C(i,w)` `i` 和`w` 会有各种不同的取值 那么我们申请一个二维数组来保存中间计算的结果
#   idx 变成了 物品数量
def package0_1_dynamic_2(idx, v, w, ws, ps):
    # 刚开始为 物品的数量
    ret_mid = [[ None for i in range(v)] for j in range(idx + 1)]
    def package0_1_inner_2(idx, v, w, ws, ps):
        if idx < 0 or v < 0:           # 这里我们做了处理 如果为0 则证明还有东西没有选的 因为 0 也是一个物品
            return 0
        print(idx,v)
        if ret_mid[idx][v - 1] is not None:       # v 的长度要减一 因为你传递过来的是 背包上线 当背包上线是10 的时候 对应 9号位置
            return ret_mid[idx][v - 1]
        ret_tmp = 0
        if  v - ws[idx] < 0:        # 表示剩下的已经不足装下现在的东西了
            ret_tmp = package0_1_inner_2(idx - 1,v, w, ws, ps)
        else:
            ret_tmp = max(ps[idx] + package0_1_inner_2(idx - 1,v - ws[idx], w, ws, ps),package0_1_inner_2(idx - 1,v, w, ws, ps))
        ret_mid[idx][v-1] = ret_tmp
        return ret_mid[idx][v-1]
    
    ret = package0_1_inner_2(idx, v, w, ws, ps)
    print(ret_mid)
    return ret

运行结果

1
2
3
4
ps = [12,3,1,3,6]
ws = [5,4,7,2,6]
ret3 = package0_1_dynamic_2(4, 10, 10, ws, ps)
# ret = 15

我们看到下面的ret_mid 数据

0 1 2 3 4 5 6 7 8 9 10
0 0 0 0 0 None 12 None 12 None 12
1 0 0 0 3 None None None 12 None 15
2 None 0 None 3 None None None 12 None 15
3 None None None 3 None None None None None 15
4 None None None None None None None None None 15

看一下依赖关系

我们根据这个图发现
第4行的图依赖于 3行的图数据 而第3行的数据依赖于第2行的数据 如果这样的话那么我们是不是可只用 两行数据来算出结果
级 i 行数据依赖于 i -1 行 ， 我们可以利用滚动数组的方法优化空间，也可以用自下而上的优化方法来优化

滚动数组的方式 好优化 只需要 将idx % 2就可以了

下面我来用自下而上的

来看代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#  
def package0_1_dynamic_3(v, ws, ps):
    max_idx = len(ws)       # 物品数量
    ret_mid = []
    # 初始化0 0 节点
    ret_zero = [0  for i in range(v + 1)]
    ret_mid.insert(0, ret_zero)
    for i in range(1,max_idx + 1):     
        ret_item = [ 0 for i in range(v + 1)]
        for vi in range(0, v + 1):
            if ws[i-1] > vi:
                ret_item[vi] = ret_mid[i - 1][vi]
            else:
                ret_item[vi]= max(ret_mid[i - 1][vi - ws[i - 1]] + ps[i - 1], ret_mid[i - 1][vi])
        ret_mid.insert(i,ret_item)
    print(ret_mid)
    return ret_mid[max_idx][v]

运行如下

1
2
3
4
ps = [12,3,1,3,6]
ws = [5,4,7,2,6]
ret3 = package0_1_dynamic_3(10, ws, ps)
print(ret3)

来看中间结果

i/v 0 1 2 3 4 5 6 7 8 9 10
0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 12 12 12 12 12 12
2 0 0 0 0 3 12 12 12 12 15 15
3 0 0 0 0 3 12 12 12 12 15 15
4 0 0 3 3 3 12 12 15 15 15 15
5 0 0 3 3 3 12 12 15 15 15 15

总结

动态规划的主要难点就是如何划分问题，将大问题拆解为子问题之后，分析子问题和原问题的最优解，然后根据问题描述拆分通项公式，最后在分析计算的冗余度。对于逻辑分析能力是个很好的锻炼。

完全背包问题

敬请期待

赏 支付宝打赏 微信打赏

赞赏一下



FEATURED TAGS
算法 动态规划
FRIENDS