大数据算法之空间亚线性算法（二）

概诉

水库抽样算法样算法虽然是抽样算法却不是近似算法。本节分享一下有限内存利用近似解求数据流中最频繁的元素。

Misra-Gries算法是频繁项挖掘中一个著名的算法。频繁项就是那些在数据流中出现频率最高的数据项。频繁项挖掘，这个看似简单的任务却是很多复杂算法的基础，同时也有着广泛的应用。

对于频繁项挖掘而言，一个简单的想法是，为所有的数据项分配计数器，当一个数据项到达，我们即增加相应计数器的值。但当数据流的规模较大时，出于内存的限制，我们往往不可能为每个数据项分配计数器。而Misra-Gries算法则是以一种清奇的思路解决了这个问题，实现了在内存受限的情况下，以较小的错误率统计数据流中的频繁项。

问题描述

先讲解一下大数据的数据流模型特点：
- 数据只能扫描1次或几次；
- 能够使用的内存是有限的（内存<<数据规模）；
- 希望通过维护一个内存结果（数据流概要）来给出相关性质的一个评估；

总结来说：数据要快速处理；空间亚线性。

问题描述
- 输入：大数据流序列<x1,x2,x3… …>。
- 输出：找出数据流中当前扫描的元素序列中出现最频繁的元素的信息。
问题定义

对于流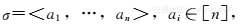隐式地定义了一个频率向量f=(f1,…,fn)。注意f1+…+fn=m。

对于一个参数k，输出集合

频繁元素问题有广泛的应用。在网络当中找到“elephant flow”、ip地址等，在搜索引擎中找到频繁查询，可以给这些最频繁的查询做一些优化。在应用当中求频繁元素时有一个假设，即**Zipf原则:典型的频率分布是高度偏斜的，只有少数频繁元素，大多数元素是非常不频繁的**。这个假设是合法的，根据统计一般最多10%的元素占元素总个数的90%。

问题分析

举个简单的例子，例如
输入： <32,12,14,32,7,12,32,7,6,12,4> 其中 n=6，k=3，m=11
- 算法如下：
  1. 对于接收到的元素x，如果已经为其分配计数器，则把相应计数器加1；
  2. 如果没有相应计数器，但计数器个数少于k,就为其分配计数器，并设为1，意味着内存中还有空间；
  3. 如果当前计数器的个数为k，说明内存已经满了，则把所有计数器减1，然后删除取值为0的计数器，这样内存就又有空间了，再依次处理下一个。
计算过程如下
- 1. 接收32，内存有空间，为其分配计数器，内存状态<32,1>。
- 1. 接收12，内存有空间，为其分配计数器，内存状态<32,1>，<12,1>。
- 1. 接收14，内存有空间，为其分配计数器，内存状态<32,1>，<12,1>,<14,1>。
- 1. 接收32，32对应计数器加1，内存状态<32,2>，<12,1>,<14,1>。
- 1. 接收7，7不在内存当中，需要为其分配新的计数器，但是内存没有空间了。这时将所有计数器减1，然后把值为0的计数器删除，这时候，12和14的计数器就没有了。注意此时不将7的计数器加1,内存状态<32,1>。
- 1. 接收12，内存又有空间，为其重新分配计数器，内存状态<32,1>，<12,1>。
- 1. 接收32，32对应计数器加1，内存状态<32,2>，<12,1>。
- 1. 接收7，为其分配计数器，内存状态<32,2>，<12,1>,<7,1>。
- 1. 接收6，这时候内存满了，把所有计数器减1，然后把值为0的计数器删除,内存状态<32,1>。
- 1. 接收12，内存又有空间，为其再重新分配计数器，内存状态<32,1>，<12,1>。
  这时候，将内存里最后的数据定为x出现的次数，计数器在内存中将x返回，没有则返回0。很显然这种方法低估了计数问题，32出现了3次，但是最后只返回1次。

算法精确性分析

代码实现

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import random
import numpy as np
import matplotlib.pyplot as plt


def getData(total = 2000):
    data = np.random.zipf(2, total)
    count_map = {}

    for value in data:
        oldValue = count_map.get(value, 0)
        oldValue +=1
        count_map[value] = oldValue
    return data,count_map

def misra_gries(S,k):
    c = {}
    for i in S:
        if i in c:
            c[i]+=1
        elif len(c)<k-1:
            c[i]=1
        else:
            for j in list(c):
                c[j]-=1
                if c[j]==0:
                    c.pop(j)
    return c



if __name__ == "__main__":
    s, cmap = getData()
    result = misra_gries(s, 10)
    
    print(result)
    print(result.keys())

总结

赏

支付宝打赏

微信打赏

赞赏一下

Misra-Gries 算法（数据流中最频繁的的数字）

概诉

问题描述

问题分析

算法精确性分析

代码实现

总结

FEATURED TAGS

FRIENDS