问题描述
- 输入:一组数据,大小未知
- 输出:这组数据的K个均匀抽取
- 要求:仅扫描一次
- 总体要求:从N个元素中随机的抽取k个元素,其中N无法确定,保证每个元素抽到的概率相同
问题难点
首先明确什么叫均匀抽样,就是每个数据被等概率抽取呗。即当样本总体为n 时候,每个样本被抽取的概率为1/n,如果要抽取k个元素,那么每个样本被抽到的概率为k/n。但是我们实现不知道总体的数量n。如果就只有n=K个元素,可用空间正好也是K,那我们正好把K个数据都保存起来,但是如果n>K呢?要想均匀抽样,概率当然是
问题解析
思路分析
假设我们有一个数据流,分别是1,2,3,起初我们并不知道这个数据流的大小。 我们要从中随机抽取一个数字,如果是均匀的抽取,每个数字被抽到的概率为1/3,首先我们需要新建一个数组,由于我们只需要取一个数据,所以数组的长度为1,现在我们有
- 未知数据流 data_stream = [1,2,3]
- 样本数组 sample = [] (长度为1)
我们开始读取数据1
sample : [1], 假设 这个时候结束,那么样本被抽取的概率为 1,既100%被抽到- 再次读取数据
2sample=[1,2],由于我们只需要一个数据,所以1 和 2 必须淘汰一个,那么如何淘汰呢?假设读到2就已经结束了,那么总体就变成了2个,2个这个时候,那么每个样本被抽取的概率就要变成1/2 才符合要求。这个时候,我们需要让2 以1/2的概率被淘汰,这样1和2被留下的概率就相等,都是1/2 满足要求。 - 再次读取数据3
sample=[?,3]因为在第二步,我们已经淘汰了1和2 所以这里用?表示被留下的那个数 即 1 或者 2。 这个时候,我们应该如何淘汰3 才能让1,2,3等概率被淘汰呢?
现在样本变成了3个,那么如果要满足提议,那必须让3 以1/3的概率留下,让3以2/3概率淘汰,那么这样来看- ?(1或者2)被留下的概率为(?留下,3淘汰)1/2 * 2/3
- 3 被留下的 概率为 1/3
- 这样刚好满足题意
- 依次类推。
来看证明:

这里做个说明:1 - 1/(i+1) = i/(i+1) 表示没有被选中的概率.
总结起来就是一句话每个数取到的概率等于取到该数且取不到该数后面所有数的概率。
如:取到第10个数的概率等于取到第十个数且取不到第11到第n个数的概率
现在我们回到较复杂的情况,也就是如何在一个N个数(开始不知道N是几)中随机取M个数。其实思想是一样的,就是先取出前M个,然后对后面的开始每个以(k/(i))的概率进行替换,这样我们得到的就是所要的结果,证明如下:

思路推广
- 从一个数据流中获取数据,保存在k个数组当中。
- 数据流中前K个数值直接保存在数组中
- 后面的在来的数据i 以 k/n 的概率 替换数组中的随机一个
代码实现
1 | #!/usr/bin/env python3 |
看一下结果
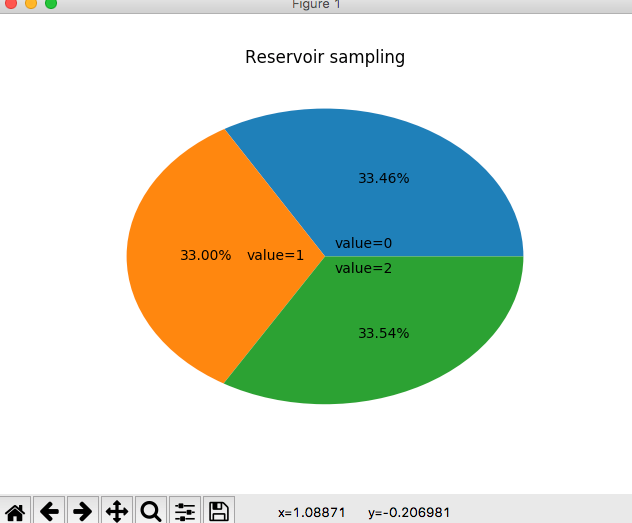
总结
赞赏一下